Minimize Cost

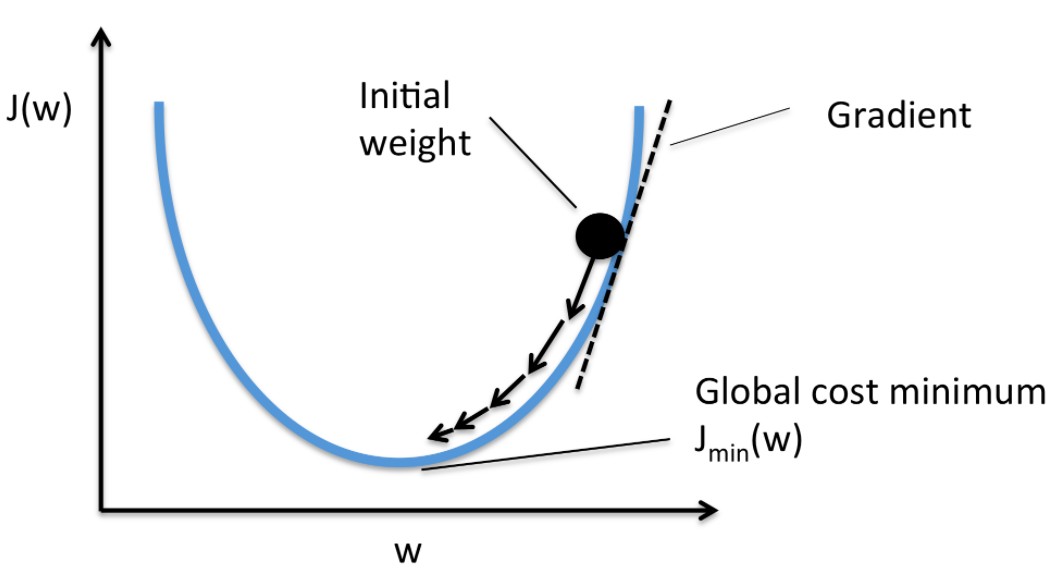역시나 처음부터 그래프를 이해할 필요 없다. 알고 싶지 않아도 저절로 알게 될테다.

Simplified Hypothesis

$H(x) = Wx$ 기울기(W)와 절편(b)으로 이루어져 있던 가설을 단순화했다. b=0으로 가정한 항태의 hypothesis 공식이다. $cost(W, b) = \frac{1}{m}\sum_{i=1}^m (H(x^i) - y^i)^2$ 다만 cost를 구하는 공식은 변하지 않는다. 우리가 예측한 X의 결과값과 실제 결과값 Y와의 차이를 비교하는 것이 골자다.

import tensorflow as tf
import matplotlib.pyplot as plt

이번에는 최적의 cost를 찾아가는 과정을 눈으로 보기 위해 시각화 패키지인 matplotlib을 사용한다.

X = [1, 2, 3]
Y = [1, 2, 3]

W = tf.placeholder(tf.float32)
# Our hypothesis for linear model W * X
hypothesis = X * W

역시나 x_data는 [1, 2, 3]이고, y_data 역시 [1, 2, 3]이다. 아직 우리가 모르는 미지의 기울기(W)는 placeholder로 node를 생성한 후 단순화한 가설 공식을 hypothesis라는 node로 구현한다.

# cost / loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))

#Launch the graph in a session
sess = tf.Session()

# Initializes global variable in the graph
sess.run(tf.global_variables_initializer())

cost를 구하는 공식도 구현하고, session을 지정해 그래프(tensor)를 그린 후 global_variables_initializer를 실행한다.(global_variables_initializer를 포함한 기본적인 내용은 앞선 포스팅에서 확인 할 수 있음.)

# Variables for plotting cost function
W_val = []
cost_val = []

for i in range(-30, 50):
    feed_W = i * 0.1
    curr_cost, curr_W = sess.run([cost, W], feed_dict = {W: feed_W})
    W_val.append(curr_W)
    cost_val.append(curr_cost)

for loop는 -30 ~ 50까지 반복되지만 코드를 잘 살펴보면 feed_W는 i에 0.1이 곱해지기 때문에 사실상 -3 ~ 5까지 반복된다. 해당 feed_W를 feed_dict에 대입하여 cost와 W 두개의 node를 실행하고 각각 cost_val, W_val 리스트에 담는다. 우리는 이 두 리스트를 사용해 시각화를 할 것이다.

# Show the cost function
plt.plot(W_val, cost_val)
plt.xlabel('weight')
plt.ylabel('cost')
plt.show()

matplotlib의 pyplot을 사용해 두 리스트의 시각화를 진행한다. 시각화를 어떻게 구현하는지는 여기서 중요한 내용이 아니므로 pass하고, 기울기(W)에 따른 cost의 변화를 그래프로 확인하는 것이 핵심 포인트다. 위와 같은 그래프가 나온다. 즉, 우리의 직관과 같이 W가 1에 가까워질수록 cost는 0에 가까워진다. 음수 또는 양수 어느 지점에서 점을 찍고 내리막길을 내려와도 1이라는 한 지점으로 수렴한다. 우리는 이제부터 이렇게 cost가 최소화되는 지점을 찾는 방식을 Gradient Descent라고 부를 것이다.

Gradient descent

$cost(W, b) = \frac{1}{m}\sum_{i=1}^m (H(x^i) - y^i)^2$ $W := W - \alpha \frac{1}{m}\sum_{i=1}^m (Wx^i - y^i) x^i$ 첫번째 공식은 우리가 만든 cost를 구하는 공식이고 두번째 공식은 첫번째 공식을 미분(derivative)한 공식이다. 미분을 못해도 괜찮다. 요새는 구글에서 공식만 입력하면 미분 공식을 만들어주는 웹사이트도 있다.

우리가 미분(derivative)을 사용하는 이유는 어렵지 않다. 앞서 도출한 그래프에서 아무 곳에서나 한 점을 찍었을 때 가장 낮은 지점으로 타고 내려올 기울기(W)를 수학적으로 구하기 위해서다. 정확한 미분 공식은 기억나지 않아도 변화량/변화량을 구하는 공식이라는 것은 기억날 것이다. 그래프 상에서 순간의 미분은 기울기(W)다.

x_data = [1, 2, 3]
y_data = [1, 2, 3]

W = tf.Variable(tf.random_normal([1]), name = "weight")
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)

# Our hypothesis for linear model W * X
hypothesis = W * X

# cost / loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))

cost가 가장 적어지는 기울기(W)를 구하기 위해 다시 초기 세팅에 들어간다. 앞서 만들었던 node와 크게 달라지는 것이 없다.

# Minimize: Gradient Descent using derivative: W -= learning rate * derivative
learning_rate = 0.1
gradient = tf.reduce_mean((W * X - Y) * X)
descent = W - learning_rate * gradient
update = W.assign(descent)

이제 우리가 미분(derivative)을 사용해 만든 공식을 코드로 구현해보자. $W := W - \alpha \frac{1}{m}\sum_{i=1}^m (Wx^i - y^i) x^i$ 일단, 미분 공식에서 $$\alpha$$는 learning_rate임을 기억하자. 어느정도의 밀도로 학습을 진행할지 정하는 상수다. gradient는 미분 공식에서 W - α 뒷부분을 구현했고, descent는 미분 공식 전체를 구현했다.

TensorFlow에서는 =을 사용해 바로 값을 지정할 수 없기 때문에 assign 메소드를 사용해 update에 담았다.

#Launch the graph in a session
sess = tf.Session()

# Initializes global variable in the graph
sess.run(tf.global_variables_initializer())
for step in range(21):
    sess.run(update, feed_dict = {X: x_data, Y: y_data})
    print(step, sess.run(cost, feed_dict = {X: x_data, Y: y_data}), sess.run(W))

실제로 cost를 낮추는 방향으로 학습이 진행되는지 알아본다. 총 20번의 session을 돌며 미분 방정식을 실행한다. 각 step마다 cost와 기울기(W)가 어떻게 변하는지 돌려보자.

1.1068848 [1.4870212]
0.31484732 [1.2597446]
0.08955658 [1.1385305]
0.025473863 [1.0738829]
0.007245909 [1.0394043]
0.0020610674 [1.0210156]
0.0005862542 [1.0112083]
0.00016675773 [1.0059777]
4.7432903e-05 [1.0031881]
1.3490738e-05 [1.0017003]
3.8373314e-06 [1.0009068]
1.0916486e-06 [1.0004836]
3.105571e-07 [1.000258]
8.8315836e-08 [1.0001376]
2.5065395e-08 [1.0000733]
7.1346826e-09 [1.0000391]
2.025999e-09 [1.0000209]
5.7622646e-10 [1.0000111]
1.6579331e-10 [1.000006]
4.7582677e-11 [1.0000032]
1.2998195e-11 [1.0000017]

회차를 거듭할 수록 cost는 0에 가까워지고 기울기(W)는 1에 수렴한다. 우리가 그래프에서 봤던 결과와 같은 결과가 나오는 것을 확인할 수 있다.

Gradient Descent Magic

여기서 드는 궁금증(이라 쓰고 걱정이라고 읽는다) 우리는 매번 cost 공식을 미분(derivative)해서 코드로 구현해야 하는 것인가. 매번… 우리가… 미분 해서… 코드로… 다행히 갓구글은 TensorFlow에서 각 상황마다 최적화된 cost를 찾아주는 패키지를 이미 만들어놨다. 예시를 통해 살펴보자.

Output when W = 5

# tf graph input
X = [1, 2, 3]
Y = [1, 2, 3]

# Set wrong model weights
W = tf.Variable(5.0)

5.0아러눈 생뚱맞은 기울기를 node로 설정해놨다. 그래프 상에서 오른쪽 위의 한 지점에 점을 찍은 것이다.

# Our hypothesis for linear model W * X
hypothesis = W * X

# cost / loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))

그리고 우리의 hypothesis 공식과 cost 공식을 구현해놨다. 여기까지는 앞선 방법과 같다. 이제부터 Magic이 펼쳐진다.

# Minimize: Gradient Descent Magic
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)

우리가 직접 미분 공식을 찾아서 코드로 만드는 대신, GradientDescentOptimizer라는 함수로 train을 시켜 optimizer라는 node를 만든다. 그리고 optimizer가 cost 공식의 결과값을 최소화시킬 수 있도록 메소드를 사용한 후 train이라는 새로운 node를 만든다.

# Launch the graph in a session
sess = tf.Session()

# Initializes global variable in the graph
sess.run(tf.global_variables_initializer())
for step in range(10):
    print(step, sess.run(W))
    sess.run(train)

이번에는 10번을 반복해서 학습을 시켜본다. 결과는.

역시나 기울기(W)가 1.0으로 수렴한다. 이제 우리가 직접 미분 공식을 찾거나 만들지 않아도 TensorFlow가 알아서 찾아준다. Gradient Descent Magic

compute_gradient & apply_gradient

이 내용은 고급 내용에 속하지만 ‘이런 것도 있구나’하고 한 번 살펴보기만 하자. 우리가 앞서 ① 직접 만든 미분 공식을 사용한 방법과 ② GradientDescentOptimizer를 사용한 방법이 다르지 않다는 것을 확인해보기 위한 방법이다. 과정이 중요할 때가 많지만 이번에는 결과만 보자.

# tf graph input
X = [1, 2, 3]
Y = [1, 2, 3]

# Set wrong model weights
W = tf.Variable(5.)

# Our hypothesis for linear model W * X
hypothesis = W * X

# Manual gradient
gradient = tf.reduce_mean((W * X - Y) * X) * 2

# cost / loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y))

# Minimize: Gradient Descent Magic
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)

미분을 사용한 직접적인 방법과 Magic을 사용한 방법 모두 코드로 구현했다.

# Get gradient
gvs = optimizer.compute_gradients(cost)
# Apply gradient
apply_gradients = optimizer.apply_gradients(gvs)

compute_gradients와 apply_gradients라는 메소드를 사용해 Gradient Descent Magic 안에서 실제 숫자가 어떻게 돌아가고 있는지 가져오라고 명령했다.

#Launch the graph in a session
sess = tf.Session()

# Initializes global variable in the graph
sess.run(tf.global_variables_initializer())

for step in range(10):
    print(step, sess.run([gradient, W, gvs]))
    sess.run(apply_gradients)

그리고 ① 직접 만든 미분 공식을 사용한 방법과 ② GradientDescentOptimizer를 사용한 방법의 각 step 별 수치를 살펴보면,

[37.333332, 5.0, [(37.333336, 5.0)]]
[2.4888866, 1.2666664, [(2.4888866, 1.2666664)]]
[0.1659259, 1.0177778, [(0.1659259, 1.0177778)]]
[0.011061668, 1.0011852, [(0.011061668, 1.0011852)]]
[0.00073742867, 1.000079, [(0.00073742867, 1.000079)]]
[4.895528e-05, 1.0000052, [(4.8955284e-05, 1.0000052)]]
[3.0994415e-06, 1.0000004, [(3.0994415e-06, 1.0000004)]]
[0.0, 1.0, [(0.0, 1.0)]]
[0.0, 1.0, [(0.0, 1.0)]]
[0.0, 1.0, [(0.0, 1.0)]]

두 결과값이 같은 것을 볼 수 있다. 즉, GradientDescentOptimizer 역시 각 공식별로 cost를 최소화하는 방법을 스스로 찾아간다는 의미다. 이제 우리는 이녀석에게 가장 작은 cost를 찾으라고 명령만 하면 된다.

가설 세우기 & 비용 함수 만들기

Hypothesis and Cost Function우리가 가지고 있는 X 값과 Y라는 결과값을 가지고서 최적의 기울기(W)와 절편(b)을 구할 수 있다면, 우리가 가지고 있지 않은 미지의 새로운 X 값에 따른 Y를 추정해볼 수 있다. X Y 1 1 2 ...

2018-04-09

@Seeyong

MachineLearning TensorFlow Coding DataScience

Introduction to Git

## What is version control?A version control system is a tool that manages changes made to the files and directories in a project. Many version control systems exist; this lesson focuses on one cal...

2018-04-12